人工知能フレームワーク入門(第5回):TensorFlowを使ったディープラーニング
前回までの記事では、TensorFlowを使って3層のニューラルネットワークを構成して機械学習による画像分類を試みた。今回は前回までのコードを拡張し、4層以上のニューラルネットワークを使用した、いわゆる深層学習(ディープラーニング)による画像分類を行う例を紹介する。
4層以上のニューラルネットワークを採用するディープラーニング
本連載第1回で紹介したように、ニューラルネットワークを用いる機械学習においては長らく多層のニューラルネットワークを効果的に扱う手法が開発されておらず、それがニューラルネットワーク技術の停滞をもたらしていた。しかし、2000年代中ごろ~後半になってこの問題を解決する複数の手法が開発されたことから多層ニューラルネットワークの研究や利用が進み、またそれがさまざまな分野において有効であることが確認されたことで普及が進んだ。TensorFlowではこのような多層ニューラルネットワークを利用するためのアルゴリズムが多数実装されており、こういった技術的背景や実装についての知識が無くとも容易に多層ニューラルネットワークを構成・利用できるようになっている。
4層のニューラルネットワークを実装する
それでは、早速4層のニューラルネットワークを使用した画像分類プログラムを説明していこう。今回の画像分類プログラムは前回記事で紹介したものと同じく、入力された画像の内容を分類するというものだ。具体的には、あらかじめ用意しておいた猫および犬、猿の写真データを使って学習を行い、続いて学習に使用したものとは異なる写真データを入力して写っている動物が猫・犬・猿のどれかを判断する、というものになる。データは猫・犬・猿それぞれ250件ずつ用意し、うち200件を学習用、50件をテスト用とした。
今回使用するコードだが、基本的な構造は前回紹介した3層のニューラルネットワークのものと同じだ(deep_lerning.py)。ただし、中間層が1層増えているので、それに伴って新たに2つめの中間層のサイズ定義(W2_SIZE)が加わっている。今回は中間層のノード数をともに100に設定した。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import sys
import os.path
import tensorflow as tf
INPUT_WIDTH = 100
INPUT_HEIGHT = 100
INPUT_CHANNELS = 3
INPUT_SIZE = INPUT_WIDTH * INPUT_HEIGHT * INPUT_CHANNELS
W1_SIZE = 100
W2_SIZE = 100
OUTPUT_SIZE = 3
LABEL_SIZE = OUTPUT_SIZE
TEACH_FILES = ["../data2/teach_cat.tfrecord",
"../data2/teach_dog.tfrecord",
"../data2/teach_monkey.tfrecord"]
TEST_FILES = ["../data2/test_cat.tfrecord",
"../data2/test_dog.tfrecord",
"../data2/test_monkey.tfrecord"]
MODEL_NAME = "./deep_model"
# 結果をそろえるために乱数の種を指定
tf.set_random_seed(1111)
モデルの定義部分については、2つの大きな変更点がある。まず1つは、中間層の2層目(第3層)として、第2層とほぼ同じ構造のものを追加したことだ。そしてもう1つは、活性化関数としてシグモイド関数(tf.sigmoid)ではなく、ReLU関数(tf.nn.relu)を使用していることだ。
## 入力と計算グラフを定義
with tf.variable_scope('model') as scope:
x1 = tf.placeholder(dtype=tf.float32)
y = tf.placeholder(dtype=tf.float32)
# 第2層
W1 = tf.get_variable("W1",
shape=[INPUT_SIZE, W1_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
b1 = tf.get_variable("b1",
shape=[W1_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
x2 = tf.nn.relu(tf.matmul(x1, W1) + b1, name="x2")
# 第3層
W2 = tf.get_variable("W2",
shape=[W1_SIZE, W2_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
b2 = tf.get_variable("b2",
shape=[W2_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
x3 = tf.nn.relu(tf.matmul(x2, W2) + b2, name="x3")
# 第4層
W3 = tf.get_variable("W3",
shape=[W2_SIZE, OUTPUT_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
b3 = tf.get_variable("b3",
shape=[OUTPUT_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
x4 = tf.nn.softmax(tf.matmul(x3, W3) + b3, name="x4")
ReLU(Rectified Linear Unit)関数はランプ関数とも呼ばれ、引数が負の場合は0、正の場合はその値をそのまま出力する関数だ。ReLUはシグモイド関数よりも出力や勾配の計算が容易で、また誤差が消失しにくいというメリットがあるため、昨今では一般的に使われている。
これ以外については前回までのコードとほぼ同一だが、最適化アルゴリズム(tf.train.GradientDescentOptimizer)の第1引数として与える学習率については前回使用した値(1e-4、0.0001)だと発散してしまい適切な値が得られなかったため、1e-6(0.000001)に変更している。
# コスト関数
cross_entropy = -tf.reduce_sum(y * tf.log(x4), name="cross_entropy")
tf.summary.scalar('cross_entropy', cross_entropy)
# 正答率
# 出力テンソルの中でもっとも値が大きいもののインデックスが
# 正答と等しいかどうかを計算する
correct = tf.equal(tf.argmax(x4,1), tf.argmax(y, 1), name="correct")
accuracy = tf.reduce_mean(tf.cast(correct, "float"), name="accuracy")
tf.summary.scalar('accuracy', accuracy)
# 最適化アルゴリズムを定義
global_step = tf.Variable(0, name='global_step', trainable=False)
optimizer = tf.train.GradientDescentOptimizer(1e-6, name="optimizer")
minimize = optimizer.minimize(cross_entropy, global_step=global_step, name="minimize")
# 学習結果を保存するためのオブジェクトを用意
saver = tf.train.Saver()
今回は学習の経過とともにテストデータに対する正答率がどう変化するのかも記録する。この処理を行うため、学習の開始前にテストデータを読み込んでおき、学習時にそれらを使って正答率をTensorBoard向けに記録するようにしている。
## テスト用データセットを読み出す
# テストデータは50×3=150件
dataset2 = tf.data.TFRecordDataset(TEST_FILES)\
.map(map_dataset)\
.batch(150)
iterator2 = dataset2.make_one_shot_iterator()
item2 = iterator2.get_next()
(testdataset_x, testdataset_y, testvalues_y) = sess.run(item2)
test_summary = tf.summary.scalar('test_result', accuracy)
また、学習にかかった時間を出力するコードも追加した。
# 学習を開始
start_time = time.time()
for i in range(30):
for j in range(100):
sess.run(minimize, {x1: dataset_x, y: dataset_y})
# 途中経過を取得・保存
xe, acc, summary = sess.run([cross_entropy, accuracy, summary_op], {x1: dataset_x, y: dataset_y})
acc2, summary2 = sess.run([accuracy, test_summary], {x1: testdataset_x, y: testdataset_y})
print("CROSS ENTROPY({}): {}".format(steps + 100 * (i+1), xe))
print(" ACCURACY({}): {}".format(steps + 100 * (i+1), acc))
print(" TEST RESULT({}): {}".format(steps + 100 * (i+1), acc2))
summary_writer.add_summary(summary, global_step=tf.train.global_step(sess, global_step))
summary_writer.add_summary(summary2, global_step=tf.train.global_step(sess, global_step))
# 学習終了
print ("time: {} sec".format(time.time() - start_time))
さて、このように実装したプログラムを使い、3000ステップの学習を行ってテストデータに対する分類処理を行った結果は次のようになった。
$ python deep_learning.py
2018-02-09 19:26:51.652084: I tensorflow/core/platform/cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: SSE4.1 SSE4.2 AVX
CROSS ENTROPY(0): 1338.601806640625
ACCURACY(0): 0.3333333432674408
CROSS ENTROPY(100): 512.6356201171875
ACCURACY(100): 0.6083333492279053
TEST RESULT(100): 0.5066666603088379
:
:
CROSS ENTROPY(3000): 1.0145809650421143
ACCURACY(3000): 1.0
TEST RESULT(3000): 0.4866666793823242
time: 366.30374217033386 sec
Model saved to ./deep_model-3000
----result with teaching data----
:
:
accuracy: 1.0
----result with test data----
assumed label:
[0 1 0 0 1 0 1 1 0 2 0 0 1 2 2 2 2 2 2 2 2 0 2 1 0 1 1 2 1 0 0 0 0 0 1 1 1
2 0 0 0 1 2 2 0 0 2 0 1 0 1 2 2 1 0 1 0 1 1 0 1 0 1 0 0 1 1 0 0 1 1 1 0 1
1 1 0 1 0 2 2 1 1 1 1 2 1 0 1 1 1 1 0 1 1 1 1 1 2 0 2 0 0 0 1 0 2 1 1 2 1
2 1 1 2 2 2 0 1 2 2 1 1 2 2 2 0 0 1 1 2 1 1 2 0 1 0 1 2 2 0 2 2 2 1 2 1 1
2 2]
real label:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
accuracy: 0.486667
ここから分かるように、学習に使用したデータ(教師データ)に対する正答率は100%となっており、学習に使用していないデータ(テストデータ)に対する正答率は48.6667%と、3層のニューラルネットワーク利用時から大幅に向上している。
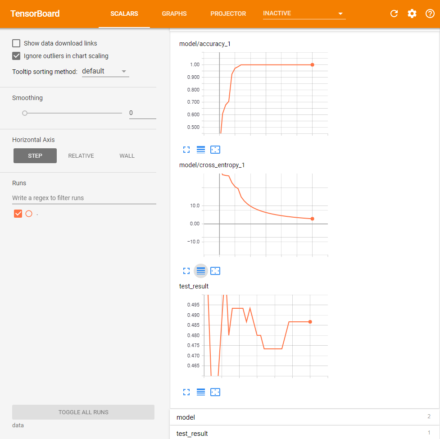
また、次のグラフは最適化処理の経過と教師データに対する正答率・クロスエントロピーの値をTensorBoardを使って表示したものだ(図1)。このグラフでは、クロスエントロピーについては縦軸を対数軸に設定している。この結果からは、教師データに対する正答率は学習に応じて順調に精度が向上していることだけでなく、テストデータに対する正答率は学習が進むにつれて上下に変動していることも分かる。
学習をより高速化・高精度化するテクニック:最適化アルゴリズムの変更
これまでは、最適化アルゴリズムとして最急降下法(tf.train.GradientDescentOptimizer)を利用していた。しかし、最急降下法では学習率の値を大きく設定しすぎると適切に探索が行えず結果が収束しないケースがある。また、逆に小さく設定しすぎると学習が遅くなってしまうという問題もあり、学習率を適切に設定するために試行錯誤が必要であった。
TensorFlowではこの最急降下法以外にも、複数の最適化アルゴリズムが実装されている。実装されているアルゴリズムは「Training」ドキュメントの「Optimizers」項にまとめられているが、この中でも収束性が高いと言われているのがtf.train.AdamOptimizerだ。アルゴリズム等については省略するが、一般的には学習率として10-3~10-4程度の値を与えるだけでより高速に最小値を探索できると言われている。
tf.train.AdamOptimizerを利用するには、最適化アルゴリズムを指定する部分でtf.train.GradientDescentOptimizerの代わりにtf.train.AdamOptimizerを指定する。
# 最適化アルゴリズムを定義 global_step = tf.Variable(0, name='global_step', trainable=False) optimizer = tf.train.AdamOptimizer(1e-4, name="optimizer") minimize = optimizer.minimize(cross_entropy, global_step=global_step, name="minimize")
このように最適化アルゴリズムを変更したプログラム(deep_lerning2.py)を実行した結果は次のようになった。
$ python deep_learning2.py
2018-02-09 19:37:50.475666: I tensorflow/core/platform/cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: SSE4.1 SSE4.2 AVX
CROSS ENTROPY(0): 1338.601806640625
ACCURACY(0): 0.3333333432674408
CROSS ENTROPY(100): 254.28439331054688
ACCURACY(100): 0.8633333444595337
TEST RESULT(100): 0.5666666626930237
:
:
CROSS ENTROPY(3000): 0.010443072766065598
ACCURACY(3000): 1.0
TEST RESULT(3000): 0.4933333396911621
time: 378.8711688518524 sec
Model saved to ./deep_model-3000
----result with teaching data----
:
:
accuracy: 1.0
----result with test data----
assumed label:
[0 1 0 2 1 0 0 1 0 2 1 2 1 2 0 0 2 0 1 0 2 0 1 0 0 1 2 0 0 0 1 0 2 0 1 1 1
0 0 1 0 0 0 2 0 0 1 0 1 0 1 2 2 1 0 2 1 1 1 0 1 0 1 0 1 1 1 0 0 1 1 2 1 1
1 1 1 0 2 2 0 2 1 1 1 2 1 0 1 1 1 1 0 1 1 2 1 1 2 2 2 0 0 0 1 2 2 1 1 2 2
2 1 1 2 2 2 0 1 1 2 0 2 1 2 2 1 0 1 0 2 1 1 1 0 1 2 0 0 1 1 2 1 1 2 2 1 1
0 2]
real label:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
accuracy: 0.493333
また、精度とクロスエントロピーの変化は次の図2のようになっている。
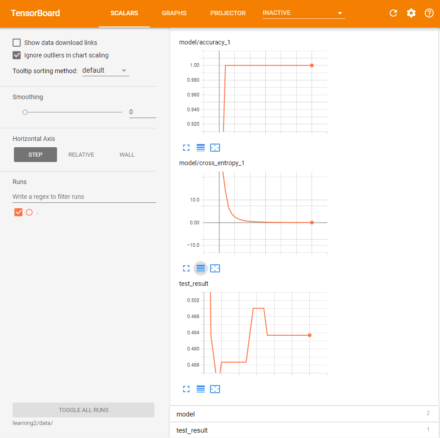
GradientDescentOptimizerを利用した場合は教師データに対する正答率が100%になるまで700回ほどの反復処理が必要だったのに対し、AdamOptimizerを利用した場合は200回ほどで正答率が100%となっている。クロスエントロピーの収束も高速で、3000ステップの反復処理実行後の正答率も49.3333%と若干ではあるが向上している。
ノード数を増やしてみる
ニューラルネットワークにおいては、ノード数を増やすことでモデルをよりよく表現できると言われている。そこで、中間層(第2層、第3層)のノード数を単純に増やして結果がどのように変化するかを確認してみた。
次の例は、基本的なコードはそのままに、中間層である第2層および第3層のノード数を次のように設定し、これまでの10倍である1000ノードに増加させて学習を行ったものだ(deep_learning3.py)。
INPUT_SIZE = INPUT_WIDTH * INPUT_HEIGHT * INPUT_CHANNELS W1_SIZE = 1000 W2_SIZE = 1000 OUTPUT_SIZE = 3 LABEL_SIZE = OUTPUT_SIZE
実行結果は次のようになった。
$ python deep_learning3.py
2018-02-09 19:50:42.301730: I tensorflow/core/platform/cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: SSE4.1 SSE4.2 AVX
CROSS ENTROPY(0): 2800.21484375
ACCURACY(0): 0.31333333253860474
CROSS ENTROPY(100): 201.76309204101562
ACCURACY(100): 0.9100000262260437
TEST RESULT(100): 0.40666666626930237
:
:
CROSS ENTROPY(3000): 0.3452143371105194
ACCURACY(3000): 1.0
TEST RESULT(3000): 0.47333332896232605
time: 3429.3428540229797 sec
Model saved to ./deep_model-3000
----result with teaching data----
:
:
accuracy: 1.0
----result with test data----
assumed label:
[0 2 0 0 2 0 0 1 0 0 0 2 0 2 0 2 2 2 0 2 1 2 2 1 0 1 1 2 0 0 2 0 1 0 2 0 0
1 0 1 0 0 2 2 0 1 2 0 2 2 1 0 2 0 2 2 0 1 1 0 1 1 0 0 1 1 2 0 0 1 1 2 1 1
1 1 1 2 0 2 2 0 1 1 1 0 1 1 1 1 2 2 0 0 1 1 1 1 0 0 0 2 0 0 1 0 2 0 1 2 1
2 0 1 2 0 2 2 2 2 2 2 2 2 2 0 0 0 2 0 2 0 0 1 0 0 0 2 2 0 1 2 1 2 2 2 1 1
1 2]
real label:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
accuracy: 0.473333
この結果から、まず3000ステップの学習処理を完了させるのにかかった時間は3429.3428540229797秒と、これまでのおよそ10倍に増えていることが分かる。一方でテストデータに対する正答率は47.3333%で、若干低下している。
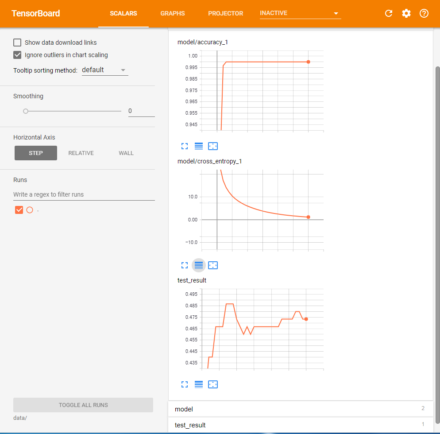
正答率の変化やクロスエントロピーの変化をTensorboardで確認すると、教師データに対する正答率やクロスエントロピーは収束しているものの、テストデータに対する正答率についてはあまり収束しておらず、単純にノードを増やしても実質的な効果は少ないようだ(図3)。
DropOutを利用する
ニューラルネットワークに対する学習では、学習処理を繰り返すことで精度が必ず向上するというわけではない。繰り返し回数が多いと、入力データに特化したネットワークになってしまい汎用性が欠けるものになってしまったり、局所的には適切だが大域的に見れば不適切な方向(局所解)に収束してしまうこともある。こういった問題は「過学習」と呼ばれており、この過学習を防ぐための複数の手法が提案されている。この1つとしてよく使われるのが、「DropOut」というものだ。DropOutは、学習の際に毎回ランダムで一定割合のノードを無効化にして最適解の探索を行うという手法だ。DropOutを利用すると、学習のステップごとに毎回ニューラルネットワークの構造が変化するため、局所解への収束を防ぐことができる。
TensorFlowではtf.nn.dropoutという関数が用意されており、容易にDropOutを組み込めるようになっている。たとえば、第1層(入力層)に対してDropoutを適用するには、次のように第1層の出力(ここではx1)を引数としてtf.nn.dropout()を適用し、その結果を第2層の入力として使用する。
# 第1層のドロップアウトを設定
x1_drop = tf.nn.dropout(x1, x1_keep_prob)
# 第2層
W1 = tf.get_variable("W1",
shape=[INPUT_SIZE, W1_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
b1 = tf.get_variable("b1",
shape=[W1_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
x2 = tf.nn.relu(tf.matmul(x1_drop, W1) + b1, name="x2")
ここで、tf.nn.dropout()の2つめの引数には無効にするノードの割合を与える。今回はx1_keep_probという変数でこれを指定した。
第2層の出力に対してもtf.nn.dropuot()を適用してその出力を第3層の入力とし、さらに第3層の出力についても同様にDropoutを適用する。
# 第2層のドロップアウトを設定
x2_drop = tf.nn.dropout(x2, x2_keep_prob)
# 第3層
W2 = tf.get_variable("W2",
shape=[W1_SIZE, W2_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
b2 = tf.get_variable("b2",
shape=[W2_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
x3 = tf.nn.relu(tf.matmul(x2_drop, W2) + b2, name="x3")
# 第3層のドロップアウトを設定
x3_drop = tf.nn.dropout(x3, x3_keep_prob)
第4層については出力層なので、Dropoutは適用しない。
# 第4層
W3 = tf.get_variable("W3",
shape=[W2_SIZE, OUTPUT_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
b3 = tf.get_variable("b3",
shape=[OUTPUT_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.01))
x4 = tf.nn.softmax(tf.matmul(x3_drop, W3) + b3, name="x4")
ちなみに、今回はenable_dropoutという変数でDropOutを利用するかどうかを設定できるようにしている。この変数に1を与えた場合はDropoutが有効、0を与えた場合は無効となる。また、DropOut有効時には第1層のノードの80%が、第2層および第3層ではノードの50%が有効になるよう設定した。
# ドロップアウト設定用のプレースホルダ
enable_dropout = tf.placeholder_with_default(0.0, [], name="enable_dropout")
# ドロップアウト確率
prob_one = tf.constant(1.0, dtype=tf.float32)
# enable_dropoutが0の場合、キープ確率は1。そうでない場合、一定の確率に設定する
x1_keep_prob = prob_one - enable_dropout * 0.2
x2_keep_prob = prob_one - enable_dropout * 0.5
x3_keep_prob = prob_one - enable_dropout * 0.5
tf.placeholder_with_default()ではデフォルト値を指定してプレースホルダを定義する関数で、今回はデフォルト値に0.0を指定した。つまり、enable_dropout変数に値が与えられなかった場合は自動的にDropOutが無効になる。これにより、たとえば学習時にはenable_dropoutに1を指定してDropOutを有効にし、正答率などの計算時にはenable_dropoutを指定せずにDropOutを無効にする、といったことが容易に行える。
# 学習を開始
start_time = time.time()
for i in range(30):
for j in range(100):
sess.run(minimize,
{x1: dataset_x,
y: dataset_y,
enable_dropout: 1.0})
# 途中経過を取得・保存
xe, acc, summary = sess.run([cross_entropy, accuracy, summary_op],
{x1: dataset_x, y: dataset_y})
acc2, summary2 = sess.run([accuracy, test_summary],
{x1: testdataset_x, y: testdataset_y})
print("CROSS ENTROPY({}): {}".format(steps + 100 * (i+1), xe))
print(" ACCURACY({}): {}".format(steps + 100 * (i+1), acc))
print(" TEST RESULT({}): {}".format(steps + 100 * (i+1), acc2))
summary_writer.add_summary(summary, global_step=tf.train.global_step(sess, global_step))
summary_writer.add_summary(summary2, global_step=tf.train.global_step(sess, global_step))
さて、このコード(deep_learning4.py)を実行した結果は次のようになった。
$ python deep_learning4.py
2018-02-15 18:22:56.745435: I tensorflow/core/platform/cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: SSE4.1 SSE4.2 AVX
CROSS ENTROPY(0): 785.1519165039062
ACCURACY(0): 0.3466666638851166
CROSS ENTROPY(100): 644.1708984375
ACCURACY(100): 0.45500001311302185
TEST RESULT(100): 0.35333332419395447
:
:
CROSS ENTROPY(3000): 8.092327117919922
ACCURACY(3000): 1.0
TEST RESULT(3000): 0.5066666603088379
time: 584.291793346405 sec
Model saved to ./deep_model-3000
----result with teaching data----
:
:
accuracy: 1.0
----result with test data----
assumed label:
[0 2 0 0 1 0 0 1 0 2 0 1 0 0 2 0 2 0 0 0 2 2 1 0 0 2 1 2 2 0 0 0 1 0 0 1 0
2 0 1 1 0 0 2 0 0 0 0 1 0 1 2 0 1 0 0 0 1 1 0 1 0 1 0 1 1 1 0 0 1 1 2 0 1
1 1 0 1 0 2 0 1 1 1 1 2 0 2 1 1 1 2 0 1 1 1 1 1 2 2 2 0 0 0 1 1 2 1 1 2 2
2 1 1 2 2 2 0 0 2 2 0 1 2 2 2 1 0 1 0 2 1 1 1 2 1 0 0 1 0 1 2 1 2 2 2 1 0
0 2]
real label:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
accuracy: 0.506667
この結果、テストデータに対する最終的な正答率は50.6667%と、数%の向上が確認できた。
TensorBoardで正答率やクロスエントロピーの変化を確認すると、教師データに対する正答率の収束やクロスエントロピーの減少はDropOutを使用しない場合と比べて遅くなっていることが分かる(図4)。
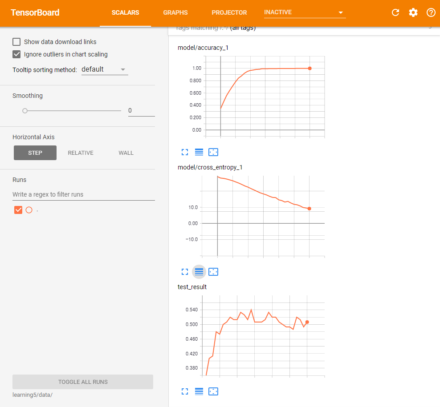
これは、DropOutを利用するとニューラルネットワークのうち一部しか学習が行われないため、学習の進みが遅くなるのが原因だ。
ミニバッチ法を使う
学習の高速化や局所解への収束を防ぐ別の手法として「ミニバッチ法」と呼ばれるものもある。これは、学習用のデータすべてをまとめて使用するのではなく、データの一部をランダムに取り出して最小値探索アルゴリズムに与えて探索(学習)を行うというものだ。
今回扱っている問題では教師データとして合計600件の画像データを使用している。今まではこれらをすべてまとめて利用していたが、たとえばバッチ数を100に設定したミニバッチ法では、600件のうちまずランダムに100件のデータを取り出し、これを利用して1ステップの学習を実行する。続いて残りの500件からランダムに100件のデータを取り出し1ステップの学習を実行する、という処理を行う。これを合計で6回繰り返すとすべての教師データを利用したことになるので、また600件のデータを読み直してランダムに100件ずつのデータを取り出す、ということを繰り返していく。
ミニバッチ法では反復処理1回あたりのデータ数が小さくなるため、学習時に必要なメモリが少なくなり、並列化もしやすいという利点がある。TensorFlowのDataset APIにはデータをランダムに取り出す機能があり、実装も比較的容易だ。
具体的には、次のようにtf.data.TFRecordDatasetクラスのインスタンス作成後、shuffle()メソッドを実行する。
## データセットの読み込み
# 読み出すデータは各データ200件ずつ×3で計600件
# 600件を読み出したあとシャッフルし、dataset_sizeで指定した
# 件数ずつ読み出す
dataset_size = tf.placeholder(shape=[], dtype=tf.int64)
dataset = tf.data.TFRecordDataset(TEACH_FILES)\
.map(map_dataset)\
.repeat()\
.shuffle(600)\
.batch(dataset_size)
shuffle()では引数としてバッファサイズを指定する。データ読み出しの際にまずここで指定した量のデータを読み出し、続いてそれらをシャッフルしてbatch()メソッドで指定した数ずつ読み出す、という仕組みになっている。そのため、引数を適切に与えないとランダム性が不足する可能性がある点には注意したい。
ちなみに、このように実行時に読み出すデータ数を変更する場合、イテレータの初期化時にパラメータを与える必要がある。そのため、イテレータの作成はmake_one_shot_iterator()ではなくmake_initializable_iterator()を利用する。
# データにアクセスするためのイテレータを作成 # 今回は繰り返しデータを初期化するので、make_initializable_iterator()で # イテレータを作成する iterator = dataset.make_initializable_iterator() next_dataset = iterator.get_next()
make_initializable_iterator()を利用する場合、イテレータの利用前にinitializerメソッドを実行することで初期化を行える。
# 学習を開始
start_time = time.time()
sess.run(iterator.initializer, {dataset_size: 100})
for i in range(90):
for j in range(100):
(dataset_x, dataset_y, values_y) = sess.run(next_dataset)
sess.run(minimize,
{x1: dataset_x,
y: dataset_y,
enable_dropout: 1.0})
なお、ミニバッチ法を利用すると一回の反復処理あたりに利用する教師データ数が少なくなる。そのため、今回は反復数を今までの3倍に相当する9000回に設定した。
さて、このようにミニバッチ法およびDropOutを利用したコード(deep_learning5.py)の実行結果は次のようになった。
$ python deep_learning5.py
2018-02-15 18:34:38.065430: I tensorflow/core/platform/cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: SSE4.1 SSE4.2 AVX
CROSS ENTROPY(0): 809.4600830078125
ACCURACY(0): 0.34333333373069763
CROSS ENTROPY(100): 649.8568725585938
ACCURACY(100): 0.4399999976158142
TEST RESULT(100): 0.36000001430511475
:
:
CROSS ENTROPY(9000): 6.498772621154785
ACCURACY(9000): 1.0
TEST RESULT(9000): 0.5533333420753479
time: 534.8445558547974 sec
Model saved to ./deep_model-9000
----result with teaching data----
:
:
accuracy: 1.0
----result with test data----
assumed label:
[0 2 0 0 0 0 0 0 0 2 0 1 0 0 0 0 2 0 0 0 1 2 2 0 0 2 1 2 2 0 0 0 2 0 0 0 0
2 0 1 1 0 0 2 0 0 0 0 1 0 1 0 2 1 1 2 0 1 1 0 1 0 1 0 1 1 1 0 0 1 1 2 0 1
1 1 0 1 0 2 0 1 1 1 1 2 1 2 1 1 1 2 0 2 1 1 1 1 1 0 2 2 0 0 1 1 2 1 1 2 2
2 1 1 2 2 2 2 0 2 2 0 1 2 2 2 0 0 2 0 2 1 0 1 0 1 0 0 0 0 1 2 1 2 0 2 1 1
0 2]
real label:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
accuracy: 0.553333
結果として、テストデータに対する正答率は55.3333%と、単にミニバッチ法を使わずにDropOutのみ利用した場合と比べて5%ほどの性能向上が見られた。また、計算時間には約535秒で、ミニバッチ法を使わない場合の約584秒よりも短くなっている。
精度やクロスエントロピーの変化グラフは次の図5のようになった。
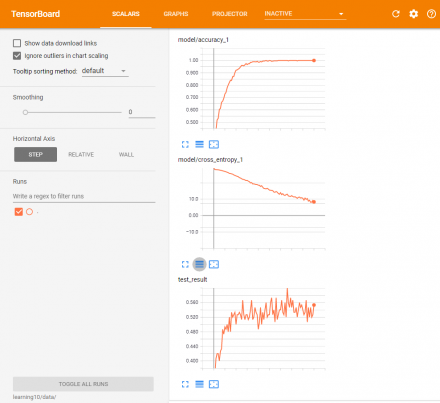
同じニューラルネットワークでも実装方法によって結果に変化
さて、今回は4層のニューラルネットワークを使って写真データの分類を試みたが、同じニューラルネットワークを利用する場合でも、ミニバッチ法やDropOutといった手法を利用することで、大きく精度が向上することが分かる。これらの手法はTensorFlowでは比較的容易に実装できるので、是非活用したいところだ。
また、ニューラルネットワークの1層あたりのノード数を増やしたケースについては、少なくとも今回の検証では精度にあまり変化を及ぼさなかった。ただ、中間層の数を増やすことで結果に大きな変化が出る可能性もある。興味のある方はぜひ検証してみるとよいだろう。
次回は、画像認識分野において有力な手法と言われている「畳み込みニューラルネットワーク」(CNN)について紹介する。