人工知能フレームワーク入門（第6回）：畳み込みニューラルネットワーク（CNN）をTensorFlowで実装する

公開日

画像分類においては、高い精度を実現できる手法として「畳み込みニューラルネットワーク（CNN）」というものが提案されている。CNNは強化学習のモデルとして使用するニューラルネットワークの形状と信号の伝達方法を工夫することで、少ないノードで高い分類能力を実現するものだ。今回はこのCNNをTensorFlowで実装したものを紹介する。

前回はシンプルに実装した4層のニューラルネットワークを使用して画像分類処理を行った。ここで使用した4層のニューラルネットワークにおいては、中間層として単純に同じ形状の層を積み上げたものを利用した。いっぽう、昨今では画像認識に適したニューラルネットワークとして、特別な形状の中間層を利用した「畳み込みニューラルネットワーク（Convolution Neural Network、CNN）」が多く使われている。

全結合によるニューラルネットワークの弱点

前回まで利用していたニューラルネットワークにおいては、中間層の各ノードにはその1つ前の層の出力すべてが入力されていた。こういったネットワークを「全結合」と呼ぶ。こういった全結合型のネットワークでは、画像の幾何学的形状についての取り扱いが明確になっていない。

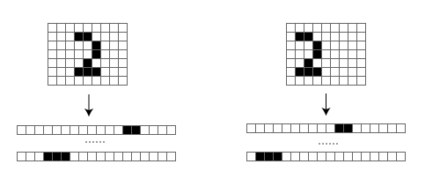
たとえば画像内に含まれた対象が平行移動しても、人間の目にはそれはほぼ同じ物と認識される。　たとえば図1は「2」という数字が描かれた画像の例だが、人間の目には右の画像も左の画像も、描かれている位置が異なるだけでまったく同じように見える。

しかし、ニューラルネットワークでこれらの画像を処理する場合、このデータは図1下のような1次元のデータに変型されて入力されるため、2次元的な情報は抜け落ちてしまう。

図1 単純な幾何学的変型でも単純なニューラルネットワークでは大きくデータが変化する
図1 単純な幾何学的変型でも単純なニューラルネットワークでは大きくデータが変化する

いっぽう、今回紹介するCNNは、画像の2次元的な情報を活用することでより高い精度を実現しようとするものだ。

畳み込みニューラルネットワークの構造

CNNでは、「畳み込み」という処理を利用することで、画像の2次元的情報を考慮したニューラルネットワークを構築して利用する。「畳み込み」という処理は画像処理分野において広く使われているもので、簡単にいうと注目した画素の周囲の画素に対し、指定された係数を掛けて加算したものを出力画素とするというものだ（図2）。

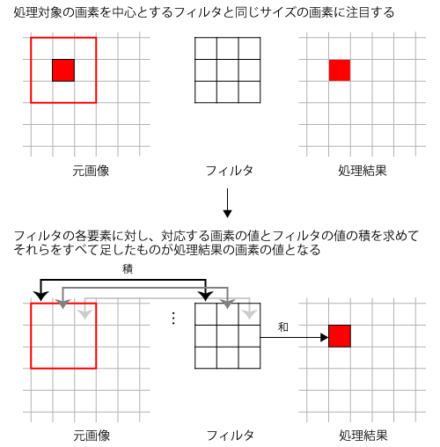
図2 畳み込み処理の概要
図2 畳み込み処理の概要

たとえば、フィルタとして3×3サイズの行列Fを使用する例を考えよう（図3）。

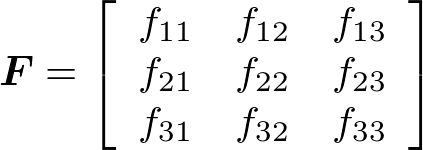
図3 フィルタとして使用する行列Fの定義
図3 フィルタとして使用する行列Fの定義

このとき、入力画像および出力画像で(x, y)という座標に対応する画素の値をそれぞれix,y、ox,yとすると、ox,yは次のようになる（図4）。

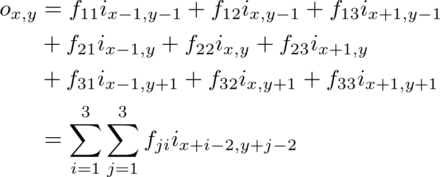
図4 畳み込み処理の数学的定義
図4 畳み込み処理の数学的定義

この処理を各画素に対して行ったものが出力画像となる。詳しくは画像処理の専門書などを参照して欲しいが、たとえばフィルタとして各要素が1/9という値の行列を使用すれば平滑化（ぼかし）を行う処理となり、中心部が正、それ以外が負の値の行列を使用すれば鮮鋭化を行う処理となる。

CNNではこの畳み込み処理をニューラルネットワークを使って実装したものを「畳み込み層」と呼び、入力に対してまずこの処理を実行する。ここで、使用するフィルタFの各要素は学習によって推定する点がポイントだ。

なお、入力が複数のチャネルを持つケースもある。たとえばカラー画像の場合、一般的には赤（R）・緑（G）・青（B）の3つのチャネル（層）を持っている。この場合、フィルタも複数の層を持ち、チャネルごとに独立して畳み込み処理を行ったあと、それらの結果を単純に加算して1つのチャネルに変換する（図5）。

図5 複数の層を持つ入力に対する畳み込み処理
図5 複数の層を持つ入力に対する畳み込み処理

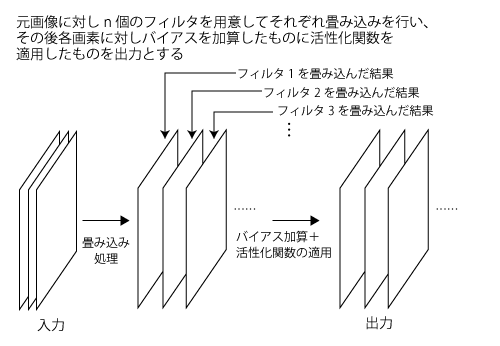
畳み込み層では通常複数個（n個）のフィルタを用意し、各フィルタを畳み込んだものに学習で推定するバイアスを加算し、活性化関数を適用した結果を出力とする。そのため、出力はn層の構造を取る（図6）。

図6 畳み込み層の処理
図6 畳み込み層の処理

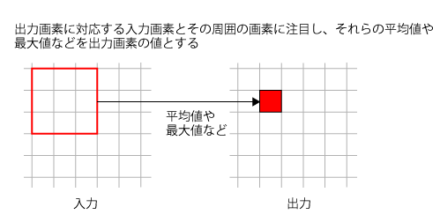
CNNでは畳み込み層に続いて、畳み込み層の出力結果に対し「プーリング」という処理を行う「プーリング層」を用意する。プーリングは簡単に言えば畳み込み層の出力結果を間引いて圧縮する処理で、畳み込み層の出力結果に対し、特定の範囲の平均値や最大値などを取り出して出力とする（図7）。

図7 データを間引く処理を行うプーリング処理
図7 データを間引く処理を行うプーリング処理

プーリング処理は畳み込みと似ているが、異なるのは入力のすべての画素に対して処理を行うのではなく、一定の間隔で画素のデータを取り出すのが特徴だ。このとき、データを取り出す間隔を「ストライド」と呼ぶ。たとえば図6はストライドを2とした例だ。

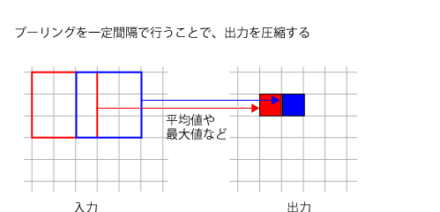
図8 ストライドを2とした場合のプーリング処理
図8 ストライドを2とした場合のプーリング処理

この場合、1画素おきにデータを取り出すようになり、入力に対し出力されるデータ数はおよそ4分の1になる（水平方向に約2分の1、垂直方向に約2分の1。入力の高さ/幅が偶数でない場合、端の部分で処理が行えないので厳密に2分の1にはならない）。

プーリング層では入力の各層に対しプーリングを行い、その結果を出力とする。このとき、前述のように各層の幅・高さはプーリングによって変化するが、層の数は変化しない（図9）。

図9 プーリング層での処理
図9 プーリング層での処理

CNNでは、この畳み込み層とプーリング層を繰り返すことで、多層のニューラルネットワークを構築する。ただし、最後の出力層では従来のニューラルネットワークのようにプーリング層の出力すべてを出力ノードに結合した構造（全結合）となる。

畳み込みニューラルネットワークの実装

それでは、CNNを実際に実装してみよう。今回実装するCNNでは、畳み込み層とプーリング層を2回繰り返す構造とした（cnn_learning.py）。また、畳み込み層での出力チャネル数は32とした。そのほかのパラメータは次のように設定している。

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import sys
import os
import tensorflow as tf
import time

# 入力画像の幅・高さ・チャネル数
INPUT_WIDTH = 100
INPUT_HEIGHT = 100
INPUT_CHANNELS = 3
INPUT_SIZE = INPUT_WIDTH * INPUT_HEIGHT * INPUT_CHANNELS

# 1つめの畳み込み-プーリング層のパラメータ
CONV1_SIZE = 5              # 畳み込みフィルタのサイズ
CONV1_STRIDE = [1, 1, 1, 1] # 畳み込みフィルタのストライド
CONV1_CHANNELS = 32         # 畳み込み層の出力チャネル数
POOL1_SIZE = [1, 2, 2, 1]   # プーリング層のウィンドウサイズ
POOL1_STRIDE = [1, 2, 2, 1] # プーリングのストライド

# 2つめの畳み込み-プーリング層のパラメータ
CONV2_SIZE = 5              # 畳み込みフィルタのサイズ
CONV2_STRIDE = [1, 1, 1, 1] # 畳み込みフィルタのストライド
CONV2_CHANNELS = 32         # 畳み込み層の出力チャネル数
POOL2_SIZE = [1, 2, 2, 1]   # プーリング層のウィンドウサイズ
POOL2_STRIDE = [1, 2, 2, 1] # プーリングのストライド

# 全結合層のサイズ
W5_SIZE=25 * 25 * CONV2_CHANNELS

# 出力サイズ
OUTPUT_SIZE = 3
LABEL_SIZE = OUTPUT_SIZE

TEACH_FILES = ["../data2/teach_cat.tfrecord",
               "../data2/teach_dog.tfrecord",
               "../data2/teach_monkey.tfrecord"]
TEST_FILES = ["../data2/test_cat.tfrecord",
              "../data2/test_dog.tfrecord",
              "../data2/test_monkey.tfrecord"]
MODEL_FILE = "./cnn_model"


# 結果をそろえるために乱数の種を指定
tf.set_random_seed(1111)

続いて、モデルの定義を行っていく。入力とラベルを入力するプレースホルダを定義する部分は今までのニューラルネットワークと同じだ。

## 入力と計算グラフを定義
with tf.variable_scope('model') as scope:

    # 入力（＝第1層）および正答を入力するプレースホルダを定義
    x1 = tf.placeholder(dtype=tf.float32, name="x1")
    y = tf.placeholder(dtype=tf.float32, name="y")

続いて畳み込み層の実装だが、ここではフィルタの各要素およびバイアスが学習変数となる。TensorFlowでは畳み込み処理がtf.nn.conv2d()として実装されており、この関数を使用するだけで計算グラフ上で畳み込み処理を実装できる。また、バイアスの加算にはtf.nn.bias_add()を利用する。

    # 第2層（畳み込み処理）
    W1 = tf.get_variable("W1",
                         shape=[CONV1_SIZE, CONV1_SIZE, INPUT_CHANNELS, CONV1_CHANNELS],
                         dtype=tf.float32,
                         initializer=tf.random_normal_initializer(stddev=0.01))

    b1 = tf.get_variable("b1",
                         shape=[CONV1_CHANNELS],
                         dtype=tf.float32,
                         initializer=tf.random_normal_initializer(stddev=0.01))
    u1 = tf.nn.bias_add(tf.nn.conv2d(x1, W1, CONV1_STRIDE, "SAME"), b1, name="u1")
    x2 = tf.nn.relu(u1, name="x2")

プーリング層では、対象の範囲から最大値を取り出す「最大値プーリング」を利用する。これは、tf.nn.max_pool()関数を利用して実装できる。

    # 第3層（プーリング層）
    x3 = tf.nn.max_pool(x2, POOL1_SIZE, POOL1_STRIDE, "SAME", name="x3")

ちなみにTensorFlowではmax_pool()だけでなく複数のプーリング関数が実装されており、関数を選択するだけで簡単にプーリング処理の内容を変えることが可能だ（TensorFlowのドキュメント）。

さて、今回は畳み込み層とプーリング層を2回繰り返す構造とするので、プーリング層の出力を2つめの畳み込み層の入力に入れて第3層、第4層を定義する。

    # 第4層（畳み込み処理）
    W3 = tf.get_variable("W3",
                         shape=[CONV2_SIZE, CONV2_SIZE, CONV1_CHANNELS, CONV2_CHANNELS],
                         dtype=tf.float32,
                         initializer=tf.random_normal_initializer(stddev=0.01))

    b3 = tf.get_variable("b3",
                         shape=[CONV2_CHANNELS],
                         dtype=tf.float32,
                         initializer=tf.random_normal_initializer(stddev=0.01))
    u3 = tf.nn.bias_add(tf.nn.conv2d(x3, W3, CONV1_STRIDE, "SAME"), b3, name="u3")
    x4 = tf.nn.relu(u3, name="x4")

    # 第5層（プーリング層）
    x5 = tf.nn.max_pool(x4, POOL2_SIZE, POOL2_STRIDE, "SAME", name="x5")

最後に、2つめのプーリング層の出力を出力層に入力する。この層の構造は今まで紹介してきたニューラルネットワークと同じ全結合となる。

    # 第6層（出力層）
    W5 = tf.get_variable("W5",
                         shape=[W5_SIZE, OUTPUT_SIZE],
                         dtype=tf.float32,
                         initializer=tf.random_normal_initializer(stddev=0.01))
    b5 = tf.get_variable("b5",
                         shape=[OUTPUT_SIZE],
                         dtype=tf.float32,
                         initializer=tf.random_normal_initializer(stddev=0.01))
    x5_ = tf.reshape(x5, [-1, W5_SIZE], name="x5_")
    x6 = tf.nn.softmax(tf.matmul(x5_, W5) + b5, name="x6")

CNNでも、コスト関数（クロスエントロピー）や正答率、最適化アルゴリズムなどの処理は全結合型のニューラルネットワークと変わらない。

    # コスト関数
    cross_entropy = -tf.reduce_sum(y * tf.log(x6), name="cross_entropy")
    tf.summary.scalar('cross_entropy', cross_entropy)

    # 正答率
    correct = tf.equal(tf.argmax(x6,1), tf.argmax(y, 1), name="correct")
    accuracy = tf.reduce_mean(tf.cast(correct, "float"), name="accuracy")
    tf.summary.scalar('accuracy', accuracy)


    # 最適化アルゴリズムを定義
    global_step = tf.Variable(0, name='global_step', trainable=False)
    optimizer = tf.train.AdamOptimizer(1e-4, name="optimizer")
    minimize = optimizer.minimize(cross_entropy, global_step=global_step, name="minimize")

データセットの読み込み部分もおおまかな流れは変わらないが、CNNの場合入力として元画像の高さ、幅、チャネルという3次元構造を保ったまま入力するため、データの読み込み後に画像データを格納したテンソルに対しtf.reshape()を実行して3次元構造を復元させている。

# 読み込んだデータの変換用関数
def map_dataset(serialized):
    features = {
        'label':     tf.FixedLenFeature([], tf.int64),
        'height':    tf.FixedLenFeature([], tf.int64),
        'width':     tf.FixedLenFeature([], tf.int64),
        'raw_image': tf.FixedLenFeature([INPUT_SIZE], tf.float32),
    }
    parsed = tf.parse_single_example(serialized, features)

    # 読み込んだデータを変換する
    raw_label = tf.cast(parsed['label'], tf.int32)
    label = tf.reshape(tf.slice(tf.eye(LABEL_SIZE),
                                [raw_label, 0],
                                [1, LABEL_SIZE]),
                       [LABEL_SIZE])

    image = tf.reshape(parsed['raw_image'], tf.stack([parsed['height'], parsed['width'], 3]))
    return (image, label, raw_label)

## データセットの読み込み
# 読み出すデータは各データ200件ずつ×3で計600件
dataset = tf.data.TFRecordDataset(TEACH_FILES)\
                 .map(map_dataset)\
                 .batch(600)

そのほかの部分は、前回までのコードとほぼ同じなので割愛する。なお、CNNは1ステップの学習に必要な計算量が全結合型のニューラルネットワークと比べて多い傾向にある。そのため、今回は10ステップの反復毎に途中経過を出力・保存するようにしている。

このコードを実行した結果は次のようになった。

$ python cnn_learning.py
2018-02-15 22:21:31.241836: I tensorflow/core/platform/cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: SSE4.1 SSE4.2 AVX
CROSS ENTROPY(0): 735.8597412109375
     ACCURACY(0): 0.39500001072883606
CROSS ENTROPY(10): 611.0742797851562
     ACCURACY(10): 0.4749999940395355
  TEST RESULT(10): 0.4000000059604645
   ：
   ：
CROSS ENTROPY(300): 1.1820317506790161
     ACCURACY(300): 1.0
  TEST RESULT(300): 0.5533333420753479
time: 2366.5111780166626 sec
Model saved to ./cnn_model
----result with teaching data----
   ：
   ：
accuracy: 1.0
----result with test data----
assumed label:
[0 2 0 1 2 0 2 0 0 2 0 1 0 2 2 2 2 0 2 2 0 0 1 0 0 1 0 0 2 1 0 0 0 1 0 1 1
 0 0 0 0 0 0 2 0 0 2 0 1 0 0 1 2 1 1 0 0 2 1 1 1 0 0 2 0 1 2 1 0 1 1 2 2 1
 1 0 1 0 0 2 0 0 1 0 2 2 1 1 1 1 1 0 0 0 1 1 1 1 2 2 2 1 2 0 1 2 2 2 1 2 2
 2 2 1 2 2 2 0 2 2 2 0 2 2 2 2 2 0 2 0 2 0 1 1 2 1 2 2 0 1 0 2 2 2 2 2 2 1
 0 2]
real label:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
accuracy: 0.553333

300回の反復処理に要した時間は約2367秒（約40分）と、前回までのものと比べて大幅に増加している。ただ、テストデータに対する最終的な正答率は55.3333％と、前回の最終的な結果とほぼ同レベルだった。また、精度やクロスエントロピーの変化は次のようになった（図10）。

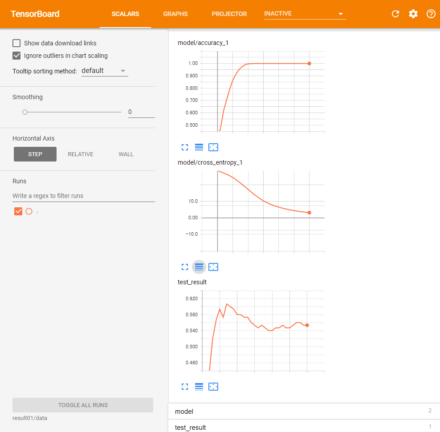
図10 正答率やクロスエントロピーの変化
図10 正答率やクロスエントロピーの変化

このグラフを見ると、テストデータに対する正答率は70ステップで約60％と最大になり、その後減少する傾向になる。これは、過学習が発生している可能性が考えられる。

CNNでのDropOut

前回記事では正答率を向上させる手法としてDropOutやミニバッチ法を紹介した。これらの手法は、CNNでも利用が可能だ。

まずDropOutについてだが、最後の全結合層にのみ適用することが一般的のようだ。コードとしては次のように第5層（2つめのプーリング層）の出力に対しtf.nn.dropout()を適用し、その結果を第6層（出力層）の入力として使用した（cnn_learning02.py）。

    # 第5層（プーリング層）
    x5 = tf.nn.max_pool(x4, POOL2_SIZE, POOL2_STRIDE, "SAME", name="x5")
    x5_ = tf.reshape(x5, [-1, W5_SIZE], name="x5_")
    x5_drop = tf.nn.dropout(x5_, x5_keep_prob, name="x5_drop")

    # 第6層（出力層）
    W5 = tf.get_variable("W5",
                         shape=[W5_SIZE, OUTPUT_SIZE],
                         dtype=tf.float32,
                         initializer=tf.random_normal_initializer(stddev=0.01))
    b5 = tf.get_variable("b5",
                         shape=[OUTPUT_SIZE],
                         dtype=tf.float32,
                         initializer=tf.random_normal_initializer(stddev=0.01))
    x6 = tf.nn.softmax(tf.matmul(x5_drop, W5) + b5, name="x6")

なお、今回はtf.nn.dropout()の第2変数には0.5を指定した。この場合、第5層のノードのうち50％がランダムで無効化されるようになる。

この場合の実行結果は次の通りだ。

$ ./cnn_learning02.py
2018-02-15 23:34:44.994726: I tensorflow/core/platform/cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: SSE4.1 SSE4.2 AVX
CROSS ENTROPY(0): 1223.6044921875
     ACCURACY(0): 0.3383333384990692
CROSS ENTROPY(100): 658.7628784179688
     ACCURACY(10): 0.4566666781902313
  ：
  ：
CROSS ENTROPY(300): 8.532224655151367
     ACCURACY(300): 1.0
  TEST RESULT(300): 0.6066666841506958
time: 2396.099194288254 sec
Model saved to ./cnn_model
----result with teaching data----
  ：
accuracy: 1.0
----result with test data----
assumed label:
[0 2 0 0 2 0 0 1 0 0 0 1 2 2 2 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0
 0 0 0 1 0 0 2 0 0 0 1 1 0 0 2 0 1 1 0 0 1 1 1 1 1 0 2 0 1 1 1 0 1 1 1 0 1
 1 1 1 0 0 2 0 1 1 0 2 2 1 1 0 1 1 0 0 0 1 1 1 1 2 1 2 2 0 2 1 2 1 2 1 2 1
 2 2 1 2 2 2 0 1 2 2 2 1 2 2 2 0 0 2 1 2 1 1 1 0 1 2 2 2 1 0 2 2 2 2 2 1 1
 0 2]
real label:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
accuracy: 0.606667

300ステップの反復処理にかかった時間は前回と同程度だが、テストデータに対する最終的な正答率は60.6667％と、5％ほどの向上が確認できた。また、精度やクロスエントロピーの変化は次のとおりだ（図11）。

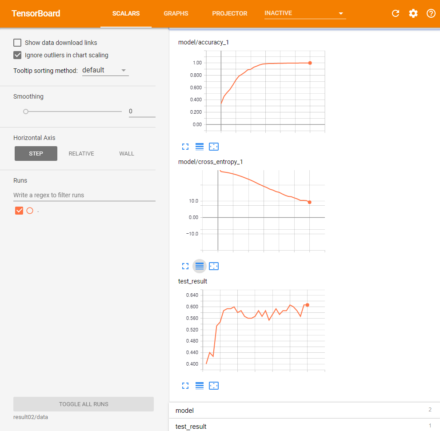
図11 正答率やクロスエントロピーの変化
図11 正答率やクロスエントロピーの変化

今回は反復回数が増えてもテストデータに対する正答率の大きな落ち込みは見られず、過学習をある程度回避できていることが確認できる。

また、次の実行例はDropOutに加えてミニバッチ法を利用するように修正した場合の結果だ（cnn_learning03.py）。ここでは反復回数を900回としている。

$ python cnn_learning03.py
2018-02-16 22:04:11.817447: I tensorflow/core/platform/cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: SSE4.1 SSE4.2 AVX
CROSS ENTROPY(0): 1151.6893310546875
     ACCURACY(0): 0.39666667580604553
CROSS ENTROPY(10): 666.7933349609375
     ACCURACY(10): 0.38999998569488525
  TEST RESULT(10): 0.40666666626930237
  ：
  ：
CROSS ENTROPY(900): 2.498356819152832
     ACCURACY(900): 1.0
  TEST RESULT(900): 0.5866666436195374
time: 1430.1005012989044 sec
Model saved to ./cnn_model
----result with teaching data----
  ：
  ：
accuracy: 1.0
----result with test data----
assumed label:
[0 2 0 0 2 0 0 0 0 0 0 0 2 2 2 0 2 1 2 0 0 0 0 0 0 1 0 0 2 0 0 0 1 0 0 1 0
 0 0 1 0 0 2 2 0 0 0 0 1 0 2 2 0 1 1 0 0 2 1 1 1 1 0 2 0 1 1 1 0 1 1 2 0 1
 1 1 0 0 0 2 0 1 1 2 2 2 1 1 1 1 2 0 0 0 1 1 1 1 2 2 2 0 0 2 1 2 1 2 1 2 2
 2 2 1 2 2 2 0 2 2 2 2 1 2 2 2 0 0 2 1 0 1 2 1 2 1 2 2 2 1 2 1 2 2 2 2 1 1
 0 2]
real label:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
accuracy: 0.586667

この場合、学習に要した時間は約1430秒（約23分）で、テストデータに対する最終的な正答率は58.6667％と、やや低下している。TensorBoardで精度やクロスエントロピーの変化を見てみると、正答率は58〜62％あたりで変化する形になっている（図12）。

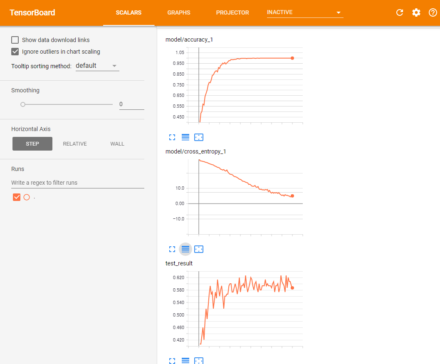
図12 正答率やクロスエントロピーの変化
図12 正答率やクロスエントロピーの変化

パラメータ調整やニューラルネットワークの構築には試行錯誤が必要

このように、ディープラーニングにCNNを利用することで実際に精度向上が見られることが確認できた。CNNは全結合型のニューラルネットワークと比べてパラメータが多いため、それらのチューニングや、畳み込み層とプーリング層をさらに追加することでより認識精度を上げることができる可能性もある。

また、ディープラーニングではこれまで紹介してきたシグモイド関数やReLU以外の活性化関数を利用することも提案されている。さらに教師データの数を増やしたり、適切に教師データを選択することでより精度を上げることも可能だろう。ちなみに、CNNを利用した画像分類では現在90％以上の精度を出すことも現実的に可能だそうだ。

AILinuxオープンソースディープラーニング機械学習
松島浩道のプロフィール画像
松島浩道
編集者/ライター（twitter：https://twitter.com/hylom、Google+：https://plus.google.com/115759524056726415451/about、本人ブログ：http://hylom.net/）。OSDN Magazine（https://osdn.jp/magazine/）およびスラド（http://srad.jp/）の編集長をこなしつつ、ITやプログラミング関連の記事執筆などを行っています。